Учимся считать в уме: умножение, деление, проценты и степени

Нюансы, которые следует учитывать

Чтобы научиться умножать двузначные числа или складывать дроби, придется потратить достаточно много времени. Однако для более быстрого обучения важно концентрировать внимание на трех основных моментах, без которых время будет потрачено впустую:

1. Концентрация внимания. Процесс обучения будет куда более эффективным, если математик научится фокусировать свое внимание на той задаче, которую выполняет, ведь очень часто приходится отвлекаться на различные внешние факторы, которые не позволяют быстро посчитать или сложить в уме сложные числа. Чтобы такого не происходило, важно научиться концентрироваться на выполнении лишь одной задачи за один раз. Для этого стоит найти для место, где никто не будет мешать, а также постараться отбросить все мысли о работе, личной жизни, планах на будущее и прочем.
2. Формулы. Чтобы производить вычисление даже сложных математических уравнений в уме, придется запомнить основные формулы и теоремы, по которым это можно сделать. Само собой, чтобы найти неизвестную переменную, иногда можно использовать и банальный метод подбора, однако такой способ является гораздо более сложным. Поэтому важно выучить всю теоретическую информацию, которую можно будет использовать: формулу дискриминанта, теорему Виета и прочие математические хитрости, с помощью которых процесс счета упрощается в несколько раз.
3. Практика. Как бы это парадоксально ни звучало, но чтобы освоить технику быстрого счета в уме, необходимо для начала научиться выполнять те же задачи на листке бумаги. Ведь записывая выполнение того или иного упражнения, можно всегда посмотреть, где именно была совершена ошибка в процессе тренировки и сделать кое-какие выводы. Как только арифметик научится легко решать сложные примеры в тетради, самое время переходить на устный счет.

Как только все правила и теоремы будут запомнены, а человек научится не только решать сложные задачи на листке бумаги, но и концентрировать свое внимание, можно приступать к процессу обучения устному счету. Под каждое математическое действие существует свой особый прием и даже несколько тренажеров, позволяющих освоить технику гораздо быстрее.

Вот и польза от интернета

Чтобы научить ребенка считать в уме, можно скачать ему на телефон специальное приложение, в котором есть огромное количество различных примеров, на решение которых дается от 2 до 5 секунд.

Само собой, можно попытаться составить уравнения и задачи самому, однако практика показывает, что в большинстве случаев они получаются крайне однообразными и не несут большой пользы.

Также существуют специальные сайты, которые позволяют своим посетителям решать уравнение и сложные задачки в режиме онлайн. Используя такие платформы, самое главное — подобрать под себя правильный уровень сложности.

Чтобы система обучения приносила как можно большую пользу, важно понять, что вовсе не обязательно часами сидеть за примерами или пытаться решить сложные задачи сразу в уме.

Ментальный счет — это долгий и кропотливый процесс, который не терпит спешки, и чтобы учиться правильно, достаточно уделять примерам от 5 до 10 минут в день. В противном случае голова будет напрягаться, а ученик начнет совершать глупейшие ошибки.

Со временем даже такое «микрообучение» приведет к потрясающим результатам. Нужно лишь набраться терпения и практиковаться согласно рекомендациям математиков.

Сложение двузначных и трехзначных чисел

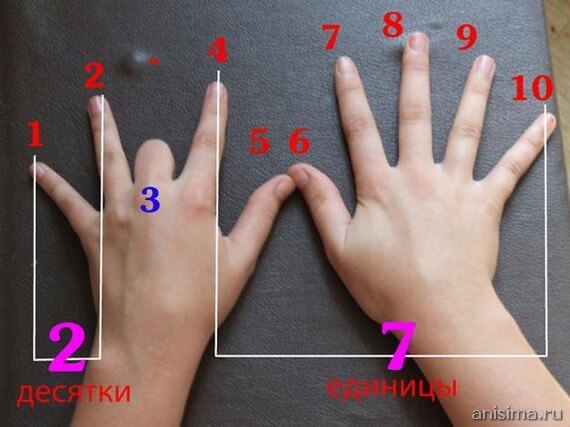
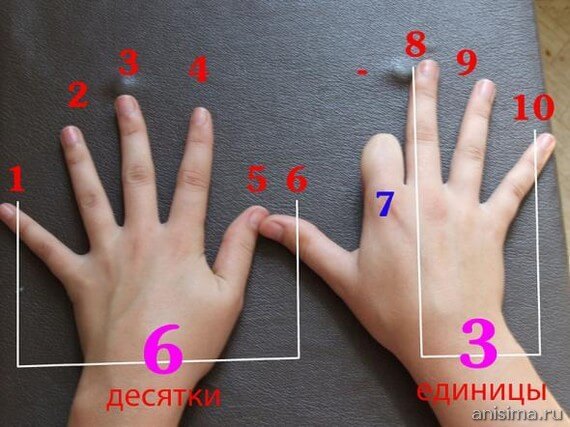
Как в первом классе детей учили быстро складывать и вычитать в уме однозначные числа? Правильно, позволяли для этого использовать пальцы. Ну а умножение и деление были освоены благодаря специальной таблице. Однако большинство взрослых, решивших научиться быстро считать в уме любые числа, как правило, умеют проводить эти действия не только с однозначными, но и с двузначными числами. В этом случае практиковаться будет значительно легче.

Однако если подросток не может сложить два двузначных числа, то сначала придется освоить именно эту методику, ведь от нее все и отталкивается. Как это сделать? Достаточно просто разбить двузначное число на десятки и единицы.

То есть если перед учеником стоит пример 65+18, то необходимо каждое число сначала разложить: 65=60+5, 18=10+8. После этого складываем в уме десятки, а уже потом единицы: 60+10=70, 5+18=13.

Если в процессе получается еще одно двузначное число, которое будет всегда состоять из одного десятка, то достаточно лишь прибавить сначала его, а уже потом — все имеющиеся единицы: 70+10=80, 80+3=83. Все довольно просто.

Однако когда речь заходит о трехзначных числах, то большинство людей почему-то сразу же входят в ступор, хотя методика здесь практически ничем не отличается от той, которая уже известна.

Для начала необходимо разбить основное число на сотни, десятки и единицы, после чего начать складывать их между собой. Вот небольшой пример: 528+376.

Действовать нужно по тому же алгоритму, что и ранее:

• Разбить числа: 528=500+20+8, 376=300+70+6.
• Сложить сотни: 500+300=800.
• Сложить десятки: 20+70=90.
• Сложить единицы 6+8=14.
• Сплюсовать все, что есть: 800+90+10+4=800+100+4=900+4=904.

Иногда, складывая десятки, также может получаться число больше сотни. Пугаться в этом случае не стоит. Достаточно будет просто прибавить одну сотню к уже имеющимся, после чего проводить арифметические действия с оставшимися десятками. Самое главное — не ошибиться в процессе.

Особенности вычитания

В математике существует всего два «полноправных» действия — сложение и умножение. Вычитание и деление являются обратными от этих двух. Кроме того, их всегда можно заменить умножением, подставив число «x», или сложением, подставив знак минус к неизвестному слагаемому. Именно поэтому, чтобы научиться вычитанию, сперва необходимо научиться складывать числа. Ведь в любой момент можно просто поменять в уме переменные и проверить правильность решения с помощью «x». Методика вычитания трехзначных чисел практически ничем не отличается от сложения. Вот небольшой пример: 553−192, а также подробный разбор:

• Разбить имеющиеся числа на сотни, десятки и единицы: 500=500+50+3, 192=100+90+2.
• Провести вычитание с сотнями: 500−100=400.
• Вычесть десятки, заняв одну сотню: 150−90=60.
• Вычесть единицы: 3−2=1.
• Сложить остатки, не забыв о заемных сотнях или десятках: «300+60+1=361».

То есть даже в вычитании будет обязательно присутствовать сложение. Основная сложность расчета таких примеров заключается в постоянной необходимости занимать десятки. Однако если проводить такую тренировку ежедневно, то со временем считать трехзначные числа будет ненамного сложнее, чем двухзначные. Самое главное — верить в себя и собственные силы.

Секреты умножения

Вот человеку нужно посчитать, находясь возле кассы, сколько же будет стоить 4 килограмма клубники по 183 рубля. Для этого он вытаскивает из кармана телефон и долго ищет в меню калькулятор.

Однако куда быстрее будет посчитать все в уме. Самое главное — знать методику, которая позволяет это делать максимально правильно, а также как можно больше практиковаться.

Алгоритм действий выглядит следующим образом.

• Разложить основное число, как и в случае с умножением: 183=100+80+3.
• Умножить число 4 на каждое имеющееся слагаемое: 100*4=400, 80*4=8*4*10=32*10=320, 3*4=12.
• Сложить все имеющиеся числа: 400+320+12=700+32=732.

Ничего сложного в этом нет, не говоря уже о том, что в умножении существует довольно много приемов, позволяющих провести операцию гораздо быстрее.

К примеру, если человеку необходимо умножить какое-то число на 25, то достаточно просто разделить его на 4, после чего умножить на 100. Вот небольшой пример: 400*25=400/4*100=100*100=10000.

Почему именно 4 и 100? Просто число 25 было замещено десятичной дробью ¼, ведь 25 — это 1 часть из 4 у сотни. Так что подобным приемом можно пользоваться, если необходимо быстро умножить что-то на «четвертак».

Сложности деления

Деление — самое сложное арифметическое действие, которое крайне трудно совершать в уме. Однако существует одна методика, которая является практически беспроигрышной. Как уже говорилось ранее, деление не является самостоятельным действием, поскольку оно обратное от умножения. Ведь что такое 32:8? Правильно: «x*8=32». Ну а по таблице умножения всем хорошо известно, что вместо переменной необходимо поставить число 4. Таким приемом можно пользоваться и для того, чтобы научиться быстро считать в уме.

Взрослому человеку это не составит большого труда, а вот ребенку придется сперва познакомиться с тем, что такое неизвестные переменные и как их искать.

Если человек научился проводить умножение с трехзначными числами в уме, то ему не составит особого труда для того, чтобы разделить эти числа. Вот небольшой пример: 795:3. Казалось бы, что посчитать его крайне трудно, но, чтобы упростить задачу, можно разбить его на множители, а также ввести переменные:

• Разбить число 795 на слагаемые, с которыми легко провести деление: «795=600+195».
• Поделить число 600 на 3 и держим в уме ответ: 200.
• Разделить число 195 на 3, но здесь необходимо также разделить его на слагаемые: 195=150+45.
• Поделить крупное число на 3: 150:3=50 и прибавляем ответ к имеющемуся: 200+50=250.
• Не зная таблицы деления, ввести переменную «x» для оставшегося числа 45=x*3. Получается, что x=15.
• Сложить остатки и проверить ответ умножением: 250+15=265, 265*3=200*3+60*3+5*3=795″ — все сходится.

Таким образом, чтобы облегчить процесс деления, можно воспользоваться не только методом разложения числа на слагаемые, но и вводя новую переменную.

Особенно полезным этот навык окажется для того, кто проводит математические действия с более интересным и сложными примерами.

Несколько месяцев практики обязательно принесут плоды, но следует взять себе за привычку проверять решение не с помощью калькулятора, а умножения.

Высчитывание процентов

Многие люди впадают в ступор, когда их просят найди 6 процентов от 253. Однако если знать основные математические правила, то в этом нет абсолютно ничего сложного. Причем, чтобы научиться проводить все действия в уме, не потребуется нескольких лет практики. Достаточно лишь следовать определенному алгоритму действий:

• Найти 1% от имеющегося числа. Для этого его необходимо разделить на 100: «253:100=2,53».
• Разложить получившиеся число на слагаемые, которые будет легко умножить на 6: 2,53=2+0,5+0,03.
• Провести умножение: 2*6=12, 0,5*6=½*6=3, 0,03*6=0,18.
• Сложить получившиеся значения: 12+3+0,18=15+0,18=15,18.

Чтобы научиться считать числа в уме, вовсе не обязательно быть вундеркиндом или потратить годы практики. Достаточно просто знать основные правила и формулы, которые позволяют упростить те или иные действия, а также уметь грамотно заменить некоторые переменные.

Ну и, пожалуй, важнее всего — концентрироваться на выполнении определенной задачи.

Если решать такие примеры каждый день, то со временем от калькулятора можно будет отказаться вовсе, что очень удобно, ведь даже в век информационных технологий полностью положиться на машины нельзя.

Источник: https://nauka.club/roditelyam/bystro-schitat-v-ume.html

Как быстро считать в уме: приемы устного счета больших чисел

Образец

Устный счет – занятие, которым в наше время себя утруждает все меньшее количество людей. Гораздо проще достать калькулятор на телефоне и вычислить любой пример.

Но так ли это на самом деле? В этой статье мы представим математические лайфхаки, которые помогут научиться быстро складывать, вычитать, умножать и делить числа в уме. Причем оперируя не единицами и десятками, а  минимум двухзначными и трехзначными числами.

После освоения методов из этой статьи идея лезть в телефон за калькулятором уже не покажется такой хорошей. Ведь можно не тратить время и посчитать все в уме гораздо быстрее, а заодно размять мозги и произвести впечатление на окружающих (противоположного пола).

Итак, добро пожаловать в увлекательный мир вычислений! Мы собрали советы от наших авторов о том, как улучшить устный счет и стать математическим героем и гением. Кстати, если вам интересна математика, вы можете почитать статью «Пределы для чайников» в нашем блоге.

Предупреждаем! Если вы обычный человек, а не вундеркинд, то для развития навыка счета в уме понадобятся тренировки и практика, концентрация внимания и терпение. Сначала все может получаться медленно, но потом дело пойдет на лад, и вы сможете быстро считать в уме любые числа.

Гаусс и устный счет

Карл Фридрих Гаусс

Одним из математиков с феноменальной скоростью устного счета был знаменитый Карл Фридрих Гаусс (1777-1855). Да-да, тот самый Гаусс, который придумал нормальное распределение.

По его собственным словам, он научился считать раньше, чем говорить.  Когда Гауссу было 3 года, мальчик взглянул на платежную ведомость своего отца и заявил: «Подсчеты неверны». После того как взрослые все перепроверили, выяснилось, что маленький Гаусс был прав.

В дальнейшем этот математик достиг немалых высот, а его труды до сих пор активно используются в теоретических и прикладных науках. До самой смерти большую часть вычислений Гаусс производил в уме.

Здесь мы не будем заниматься сложными расчетами, а начнем с самого простого.

Сложение чисел в уме

Чтобы научиться складывать в уме большие числа, нужно уметь безошибочно складывать числа до 10. В конечном счете любая сложная задача сводится к выполнению нескольких тривиальных действий.

Чаще всего проблемы и ошибки возникают при сложении чисел с «переходом через 10». При сложении (да и при вычитании) удобно применять технику «опоры на десяток». Что это? Сначала мы мысленно спрашиваем себя, сколько одному из слагаемых не хватает до 10, а потом прибавляем к 10 оставшуюся до второго слагаемого разность.

Например, сложим числа 8 и 6. Чтобы из 8 получить 10, не хватает 2. Затем к 10 останется прибавить 4=6-2. В итоге получаем: 8+6=(8+2)+4=10+4=14

Пусть нам нужно сложить два числа: 356 и 728. Число 356 можно представить как 300+50+6.  Аналогично, 728 будет иметь вид 700+20+8. Теперь складываем:

356+728=(300+700)+(50+20)+(8+6)=1000+70+14=1084

Вычитание чисел в уме

Вычитание чисел тоже будет даваться легко. Но в отличие от сложения, где каждое число разбивается на разрядные части, при вычитании «разбить» нужно только то число, которое мы отнимаем.

Например, сколько будет 528-321? Разбиваем число 321 на разрядные части и получаем: 321=300+20+1.

Теперь считаем: 528-300-20-1=228-20-1=208-1=207

Попробуйте визуализировать процессы сложения и вычитания. В школе всех учили считать в столбик, то есть сверху вниз. Один из способов перестроить мышление и ускорить счет – считать не сверху вниз, а слева направо, разбивая числа на разрядные части.

Умножение чисел в уме

Умножение – это многократное повторение числа. Если нужно умножить 8 на 4, это значит, что число 8 нужно повторить 4 раза.

8*4=8+8+8+8=32

Так как все сложные задачи сводятся к более простым, нужно уметь умножать все однозначные числа. Для этого существует отличный инструмент – таблица умножения. Если вы не знаете эту таблицу на зубок, то мы настоятельно рекомендуем первым делом выучить ее и только потом приниматься за практику устного счета. К тому же учить там, по сути, нечего.

Таблица умножения

Умножение многозначных чисел на однозначные

Сначала потренируйтесь в умножении многозначных чисел на однозначные. Пусть нужно умножить 528 на 6. Разбиваем число 528 на разряды и идем от старшего к младшему. Сначала умножаем, а потом складываем результаты.

• 528=500+20+8
• 528*6=500*6+20*6+8*6=3000+120+48=3168
• Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Умножение двузначных чисел

Здесь тоже нет ничего сложного, только нагрузка на краткосрочную память немного больше.

Перемножим 28 и 32. Для этого сведем всю операцию к умножению на однозначные числа. Представим 32 как 30+2

28*32=28*30+28*2=20*30+8*30+20*2+8*2=600+240+40+16=896

Еще один пример. Умножим 79 на 57. Это значит, что на нужно взять число «79» 57 раз. Разобьем всю операцию на этапы. Сначала умножим 79 на 50, а потом – 79 на 7.

• 79*50=(70+9)*50=3500+450=3950
• 79*7=(70+9)*7=490+63=553
• 3950+553=4503

Умножение на 11

Вот хитрый прием быстрого устного счета, который поможет умножить любое двузначное число на 11 с феноменальной скоростью.

Чтобы умножить двузначное число на 11, две цифры числа складываем друг с другом, и получившуюся сумму вписываем между цифрами исходного числа. Получившееся в итоге трехзначное число — результат умножения исходного числа на 11.

Проверим и умножим 54 на 11.

Возьмите любое двузначное число, умножьте его на 11 и убедитесь сами — эта хитрость работает!

Возведение в квадрат

С помощью другого интересного приема устного счета можно легко и быстро возводить двузначные числа в квадрат. Особенно просто это делать с числами, которые заканчиваются на 5.

Результат начинается с произведения первой цифры числа на следующую за ней по иерархии. То есть, если эту цифру обозначить через n, то следующей за ней по иерархии цифрой будет n+1. Результат заканчивается на квадрат последней цифры, то есть квадрат 5.

Проверим! Возведем в квадрат число 75.

Раньше все считали без калькуляторов

Деление чисел в уме

Осталось разобраться с делением. По сути, это операция, обратная умножению. С делением чисел до 100 никаких проблем вообще возникать не должно – ведь есть таблица умножения, которую вы знаете на зубок.

Деление на однозначное число

При делении многозначных чисел на однозначное необходимо выделить максимально большую часть, которую можно разделить с помощью таблицы умножения.

Например, есть число 6144, которое нужно разделить на 8. Вспоминаем таблицу умножения и понимаем, что на 8 будет делиться число 5600. Представим пример в виде:

1. 6144:8=(5600+544):8=700+544:8
2. Далее из числа 544 также выделяем максимально большое число, которое делится на 8. Имеем:
3. 544:8=(480+64):8=60+64:8
4. Осталось разделить 64 на 8 и получить результат, сложив все результаты деления
5. 64:8=8
6. 6144:8=700+60+8=768

Деление на двузначное число

При делении на двузначное число нужно пользоваться правилом последней цифры результата при умножении двух чисел.

При умножении двух многозначных чисел последняя цифра результата умножения всегда совпадает с последней цифрой результата умножения последних цифр этих чисел.

Например, умножим 1325 на 656. По правилу, последняя цифра в получившемся числе будет , так как 5*6=30. Действительно, 1325*656=869200.

Теперь, вооружившись этой ценной информацией, рассмотрим деление на двузначное число.

Сколько будет 4424:56?

Первоначально будем пользоваться методом «подгона» и найдем пределы, в которых лежит результат. Нам нужно найти число, которое при умножении на 56 даст 4424. Интуитивно попробуем число 80.

56*80=4480

Значит, искомое число меньше 80 и явно больше 70. Определим его последнюю цифру. Ее произведение на 6 должно заканчиваться цифрой 4.

Согласно таблице умножения, нам подходят результаты 4 и 9. Логично предположить, что результатом деления  может быть либо число 74, либо 79.

Проверяем:

Готово, решение найдено! Если бы не подошло число 79, второй вариант обязательно оказался бы верным.

Картина Н.П. Богданова-Бельского «Устный счёт. В народной школе С. А. Рачинского»

Полезные советы

В заключение приведем несколько полезных советов, которые помогут быстро научиться устному счету:

• Не забывайте тренироваться каждый день;
• не бросайте тренировки, если результат не приходит так быстро, как хотелось бы;
• скачайте мобильное приложение для устного счета: так вам не придется самостоятельно придумывать себе примеры;
• почитайте книги по методикам быстрого устного счета. Существуют разные техники устного счета, и вы сможете овладеть той, которая лучше всего подходит именно вам.

Польза устного счета неоспорима. Тренируйтесь, и с каждым днем вы будете считать все быстрее и быстрее. А если вам понадобится помощь в решении более сложных и многоуровневых задач, обращайтесь к специалистам студенческого сервиса за быстрой и квалифицированной помощью!

Источник: https://Zaochnik-com.ru/blog/kak-bystro-schitat-v-ume-priemy-ustnogo-scheta-bolshix-chisel/

Приемы быстрого счета без калькулятора

Хоть и считается, что математика наводит ужас на значительную часть населения, но деньги считать умеют все. И вот как раз влет это умеют делать люди, далекие от математики.

Помнится, бабушка моего мужа показывала ему на пальцах таблицу умножения на 9. Никакого образования, только огромная практика торговли редиской и клубникой на рынке!

Так вот сегодня я предлагаю вам несколько интересненьких приемов устного счета. Ведь сколько бы замечательных гаджетов (телефоны, смартфоны, айподы и айпады, ай, да чего там…) своя голова она всегда лучше.

Итак, читаем, тут же проверяем и запоминаем приемы вычисления в уме.

1. Умножение на 11

• Умножать на 11 чуть сложнее, чем умножать на 10. Закономерность здесь такая:
• 53 х 11 = 583
  Шаг 1 — Складываем две цифры двузначного числа: 5 + 3 = 8
• Шаг 2 — Помещаем результат между двумя числами двузначного числа: 583

59 х 11 = 649
Шаг 1 — 5 + 9 = 14
Шаг 2 — Перекидываем единицу налево, если сумма на предыдущем шаге оказалась больше 9: 5 + 1 = 6 (справа остается второй символ, в данном случае это четверка)

Шаг 3 — На первый символ мы единицу уже перекинули, получили 6. Далее у нас осталась 4, которую ставим в центр, и дописываем 9: 649

2. Быстрое возведение в квадрат

1. Этот прием поможет быстро возвести в квадрат двузначное число, которое заканчивается на 5.
2. 85 х 85 = 7225
   Шаг 1 — Умножаем первую цифру на первую цифру, увеличенную на единицу: 8 x (8 + 1) = 72
3. Шаг 2 — Дописываем к получившемуся результату 25: 7225
4. 45 x 45 = 2025
   Шаг 1 — 4 х (4 + 1) = 20
5. Шаг 2 — 2025

3. Умножение на 5

Большинство людей очень просто запоминает таблицу умножения на 5, но, когда приходится иметь дело с большими числами, сделать это становится сложнее. Или нет? Этот прием невероятно прост.

Возьмите любое число, разделите на 2 (другими словами, поделите пополам). Если в результате получилось целое число, припишите 0 в конце. Если нет, не обращайте внимание на запятую и в конце добавьте 5.

Это срабатывает всегда:
2682×5 = (2682 / 2) & 5 или 0
2682 / 2 = 1341 (целое число, поэтому добавьте 0)
13410
Давайте попробуем другой пример:
5887×5
2943,5 (дробное число, пропустите запятую, добавьте 5)

29435

4. Умножение на 9

Это просто. Чтобы умножить любое число от 1 до 9 на 9, посмотрите на руки. Загните палец, который соответствует умножаемому числу (например 9×3 – загните третий палец), посчитайте пальцы до загнутого пальца (в случае 9×3 – это 2), затем посчитайте после загнутого пальца (в нашем случае – 7). Ответ – 27.

5. Умножение на 4

Это очень простой прием, хотя очевиден лишь для некоторых. Хитрость в том, что нужно просто умножить на 2, а затем опять умножить на 2:
58×4 = (58×2) + (58×2) = (116) + (116) = 232

6. Подсчет чаевых

Если вам нужно оставить 15% чаевых, есть простой способ сделать это.

Высчитайте 10% (разделите число на 10), а потом добавьте получившееся число к его половине и получите ответ:
15% от $25 = (10% от 25) + ((10% от 25) / 2)

$2.50 + $1.25 = $3.75

• И, как следствие):  чтобы умножить число на 1,5 нужно к исходному числу прибавить его половину. Например,
• 34*1,5 = 34+17=51
• 125*1,5= 125+62,5=187,5

7. Сложное умножение

Если вам нужно умножать большие числа, причем одно из них — четное, вы можете просто перегруппировать их, чтобы получить ответ:
32×125 все равно, что:
16×250 все равно, что:
8×500 все равно, что:

4×1000 = 4,000

8. Деление на 5

На самом деле делить большие числа на 5 очень просто. Все, что нужно,— просто умножить на 2 и перенести запятую: 195 / 5
Шаг1: 195×2 = 390
Шаг2: Переносим запятую: 39,0 или просто 39.
2978 / 5
Шаг1: 2978×2 = 5956

Шаг2: 595,6

9. Вычитание из 1000

1. Чтобы выполнить вычитание из 1000, можете пользоваться этим простым правилом: Отнимите от 9 все цифры, кроме последней. А последнюю цифру отнимите от 10:
2. 1000-648
3. Шаг1: от 9 отнимите 6 = 3
   Шаг2: от 9 отнимите 4 = 5
   Шаг3: от 10 отнимите 8 = 2
4. Ответ: 352
5. И, напоследок, несколько математических трюков:

Интересные результаты:

• 1 х 1 = 1
  11 х 11 = 121
  111 х 111 = 12321
  1111 х 1111 = 1234321
  11111 х 11111 = 123454321
  111111 х 111111 = 12345654321
  1111111 х 1111111 = 1234567654321
  11111111 х 11111111 = 123456787654321
• 111111111 х 111111111 = 12345678987654321
• 1 х 9 + 2 = 11
  12 х 9 + 3 = 111
  123 х 9 + 4 = 1111
  1234 х 9 + 5 = 11111
  12345 х 9 + 6 = 111111
  123456 х 9 + 7 = 1111111
  1234567 х 9 + 8 = 11111111
  12345678 х 9 + 9 = 111111111
• 123456789 х 9 + 10 = 1111111111
• 9 х 9 + 7 = 88
  98 х 9 + 6 = 888
  987 х 9 + 5 = 8888
  9876 х 9 + 4 = 88888
  98765 х 9 + 3 = 888888
  987654 х 9 + 2 = 8888888
  9876543 х 9 + 1 = 88888888
• 98765432 х 9 + 0 = 888888888
• 1 х 8 + 1 = 9
  12 х 8 + 2 = 98
  123 х 8 + 3 = 987
  1234 х 8 + 4 = 9876
  12345 х 8 + 5 = 98765
  123456 х 8 + 6 = 987654
  1234567 х 8 + 7 = 9876543
  12345678 х 8 + 8 = 98765432
• 123456789 х 8 + 9 = 987654321

Любимая цифра.

Предложите  задумать свою любимую цифру. А теперь выполните умножение (на калькуляторе) числа 15873 на любимую цифру, умноженную на 7. Например, если любимая цифра 5, то умножить нужно на 35. Получится произведение, записанное только любимой цифрой.

Возможен и второй вариант: умножить число 12345679 на любимую цифру, умноженную на 9, в нашем случае это число 45.

Объяснение этого фокуса достаточно простое: если умножить 15873 на 7, то получится 111111, а если умножить 12345679 на 9, то получится 111111111.

Угадать возраст.

Умножаем число своих лет на 10, затем любое однозначное число умножить на 9,  из первого произведения вычесть второе и сообщить полученную разность. В этом числе “фокусник” должен цифру единиц сложить с цифрой десятков – получится число лет.

Всегда девятка

Предложите кому-нибудь написать число из трех разных цифр, под ним — написать число из этих же цифр, но в обратном порядке. Затем вычесть меньшее из большего. Когда зритель это сделает, скажите ему, что в середине числа стоит девятка.

Секрет фокуса: Вы будете правы, потому что девятка всегда будет в середине независимо от того, какие цифры написаны.

Источник: https://anisim.org/articles/priemy-bystrogo-scheta-bez-kalkulyatora/

22 простых способа научиться быстро считать в уме

Добрый день! Много вопросов поступает от школьников по разным предметам. Сегодня поговорим о том, как быстро считать в уме, чтобы легко решать разные примеры и задачи по математике.

Материал также будет полезен взрослым, ведь нам тоже приходится немало высчитывать в уме в быту. А еще это улучшает мозговую активность, концентрацию, внимание и память.

Читаем, изучаем, учимся легко и интересно.

Надеюсь, что вам будет понятно и обязательно пригодится на деле. Жду ваших комментариев, пальчиков вверх и репостов!

Вступление

В современном мире с множеством сверх прогрессивных девайсов, счет в уме не утратил своей актуальности.

Как научиться быстро считать в уме? Предложенные в данной статье методики помогут вам развить феноменальный талант быстрого счета.

Три составляющих успешного обучения

• Способности. Для того чтобы научиться считать в уме, следует уметь концентрировать внимание на поставленной задаче и удерживать в памяти сложные числа.
• Формулы. Чтобы легко и просто производить вычисления в уме, следует запомнить основные математические формулы.
• Практика. Частые тренировки позволят развить и усовершенствовать навык.

• Учимся устно умножать на 11
• Существует несколько простых способов умножения числа на 11.
• Способ 1
• При умножении 2-значного числа на 11, раздвинем цифры множителя.
• Например (54 * 11):
  5 _ 4 * 11=…
• Теперь суммируем единицы и десятки, а полученный результат записываем в ответе:
  5 (5+4) 4 * 11 = 5 (9) 4 = 594
• Например (89 * 11):
  8 _ (8+9) _9 = 8 _ (17) _ 9 = _ (8+1) _ 79 = 979
• Способ 2
• При умножении на 11 разложим число 11 на сумму: 10+1, и произведем умножение частей.
• Например:
  12 * 11 = 12 * (10+1) = 120 + 12 = 132
• Так же и с 3-значными числами:
  114 * 11 = 114 * (10+1) = 1140 + 114 = 1254

Умножаем на 9 и 11

Примеры:
15 * 9 = 15 * 10 – 15 = 150 — 15 = 135
57 * 11 = 57 * 10 + 57 = 570 + 57 = 627

Возведение в квадрат числа, заканчивающегося на 5

Достаточно простая методика. Умножаем десяток на самого себя +1, и дописываем «25» в конце.

Например (35 * 35):
35 * 35 = 3 * (3+1)_25 = 1225

Устное умножение на 5, 25, 50, 125

Умножить на 5 числа до 10-ти не составляет проблем

Давайте научимся так же легко умножать двузначные и трехзначные числа.

Способ 1

Разделим наш множитель на «2». Получилось целое число? Значит, добавим к нему в конце «0», если число поровну не делится – отбрасываем остаток и добавляем «5» в конце.

1. Например (1482 * 5):
   1482 * 5 = (1482/2) _ (+0 или +5) = 741 _(+0) = 7410 – число делится на 2 без остатка
2. 2269 * 5 = (2269/2) _ (+0 или +5) = 1134.5 _ (+5) = 11345 – число делится на 2 с остатком
3. Способ 2
4. Умножая число на 5, 25, 50, 125 можно использовать следующие формулы:
   А * 5 = А * 10 / 2
   А * 50 = А * 100 / 2
   А * 25 = А * 100 / 4
5. А * 125 = А* 1000 / 8
6. Примеры:
   44 * 5 = 44 * 10 / 2 = 440 / 2 = 220
   24 * 50 = 24 * 100 / 2 = 2400 / 2 = 1200
   26 * 25 = 26 * 100 / 4 = 2600 / 4 = 650
7. 54 * 125 = 54 * 1000 / 8 = 54000 / 8 = 6750

Учимся устно умножать на 4

• Достаточно простой метод, не требующий особых усилий.
• Умножаем число на «2», а потом полученный результат снова умножаем на «2».
• Например:
  27 * 4 = 27 * 2 * 2 = 54 * 2 = 108
• Вычисляем в уме 15 % от числа
• Находим 10% от числа и добавляем ½ от 10%.

Например:
15% от 664 = (10% ) + (10% / 2) = 66.4 + 33.2 = 99.6

Умножаем в уме большие числа, одно из которых четное

Например:
48 * 125 = 24 * 250 = 12 * 500 = 6 * 1000 = 6000

Учимся делить на 5, 50, 25

1. Один простой прием поможет вам быстро делить в уме: умножим наше число на «2» и переместим запятую на одну цифру назад.

2. 145 / 5 = 145 * 2 = 290 (смещаем запятую) = 29
   1200 / 5 = 1200 * 2 = 2 400 (смещаем запятую) = 240
3. При делении на 50, 25, удобно воспользоваться формулами:
4. А / 50 = А * 2 / 100
   А / 25 – А * 4 / 100
5. Примеры:
   2350 / 50 = 2350 * 2 / 100 = 4700 / 100 = 47
6. 2600 / 25 = 2600 * 4 / 100 = 10400 / 100 = 104

Вычитаем из 1000

Для того, чтобы вычесть число из 1000, отнимаем каждую цифру числа от «9», а последнюю цифру отнимаем от 10.

Например:
1000 – 248 = (9-2) _ (9-4) _ (10-8) = 752

Умножаем простые числа

Пример, умножим 7 на 8: 3 __ 2
7 8
8 – 3 = 5 _
3 * 2 = 6

Итог: 56

Умножаем числа от 10 до 20

Для того чтобы быстро в уме умножать числа от 10 до 20-ти, следует знать одну хитрость: к одному числу прибавим единицы другого, а сумму умножим на 10, к полученному результату добавим произведение единиц.

Пример:
13 * 15 = (13 + 5) * 10 + 3 * 5 = 180 + 15 = 195

Складываем и вычитаем натуральные числа

1. Если слагаемое увеличить на некоторое число, то это же число следует вычесть из полученной суммы.

Например:
650 + 346 = (650 + 346 + 4) – 4 = (650 + 350) – 2 = 1000 – 2 = 998

2. Если одно слагаемое уменьшить на некоторое число, а ко второму слагаемому это же число добавить, то сумма не изменится.

Например:
335 + 765 = (335 + 5) + (765 — 5) = 340 + 760 = 1100

3. Если к уменьшаемому и вычитаемому добавить одно и то же число, результат не изменится.

Например:
225 — 339 = (225 + 5) — (339 + 5) = 230 — 344 = 114

Умножаем числа с одинаковым количеством десятков, сумма единиц которых = 10

Например:
302 * 308 = ..
1). 30 * (30 + 1) = 900 + 30 = 930
2). 2 * 8 = 16

Умножаем на число, состоящее из цифр 9

Как умножить на число 9, 99, 999?

• Для этого просто добавим недостающие единицы и произведем вычисление.
• Пример:
  154 * 99 = 154 * (100 — 1) = 15400 — 154 = 15246
• Складываем близкие по величине числа
• Производим вычисление ряда чисел, близких по величине
• Их можно разложить, и сложить частями.
• Например:
  19 + 22 + 23 + 21+ 24 + 17=…
• Разложим слагаемые:
  19 = 20 — 1
  22 = 20 + 2
  23 = 20 + 3
  21 = 20 + 1
  24 = 20 + 4
• 17 = 20 -3
• Итог: 20 * 6 + (2-1+3+1+4-3) = 120 + 6 = 126

Надеемся, что наши советы помогут вам освоить приемы быстрого счета в уме.

Следует помнить, что теория – это лишь 20 % успеха. Остальные 80% — ваше желание и практика.

[Источник: http://domznaniy.ru/]

Несколько полезных советов

Источник: http://1obuchenie.com/kak-nauchitsya-bystro-schitat-v-ume.html

10 трюков, упрощающих математические операции — «Хакер»

Рекомендуем почитать:

• Содержание выпуска
• Подписка на «Хакер»

В книге «Магия чисел» рассказывается о десятках трюков, которые упрощают привычные математические операции. Оказалось, что умножение и деление в столбик — это прошлый век, а есть гораздо более эффективные способы деления в уме.

Вот 10 самых интересных и полезных трюков.

Умножение «3 на 1» в уме

Умножение трёхзначных чисел на однозначные — это очень простая операция. Всё, что нужно сделать, — это разбить большую задачу на несколько маленьких.

Пример: 320 × 7

1. Разбиваем число 320 на два более простых числа: 300 и 20.
2. Умножаем 300 на 7 и 20 на 7 по отдельности (2 100 и 140).
3. Складываем получившиеся числа (2 240).

Возведение в квадрат двузначных чисел

Возводить в квадрат двузначные числа не намного сложнее. Нужно разбить число на два и получить приближенный ответ.

Пример: 41^2

1. Вычтем 1 из 41, чтобы получить 40, и добавим 1 к 41, чтобы получить 42.
2. Умножаем два получившихся числа, воспользовавшись предыдущим советом (40 × 42 = 1 680).
3. Прибавляем квадрат числа, на величину которого мы уменьшали и увеличивали 41 (1 680 + 1^2 = 1 681).

Ключевое правило здесь — превратить искомое число в пару других чисел, которые перемножить гораздо проще. К примеру, для числа 41 это числа 42 и 40, для числа 77 — 84 и 70. То есть мы вычитаем и прибавляем одно и то же число.

Мгновенное возведение в квадрат числа, оканчивающегося на 5

С квадратами чисел, оканчивающихся на 5, вообще не нужно напрягаться. Всё, что нужно сделать, — это умножить первую цифру на число, которое на единицу больше, и добавить в конец числа 25.

Пример: 75^2

Умножаем 7 на 8 и получаем 56.

Добавляем к числу 25 и получаем 5 625.

Деление на однозначное число

Деление в уме — это достаточно полезный навык. Задумайтесь о том, как часто мы делим числа каждый день. К примеру, счёт в ресторане.

Пример: 675 : 8

1. Найдём приближенные ответы, умножив 8 на удобные числа, которые дают крайние результаты (8 × 80 = 640, 8 × 90 = 720). Наш ответ — 80 с хвостиком.
2. Вычтем 640 из 675. Получив число 35, нужно разделить его на 8 и получить 4 с остатком 3.
3. Наш финальный ответ — 84,3.

Мы получаем не максимально точный ответ (правильный ответ — 84,375), но согласитесь, что даже такого ответа будет более чем достаточно.

Простое получение 15%

Чтобы быстро узнать 15% от любого числа, нужно сначала посчитать 10% от него (перенеся запятую на один знак влево), затем поделить получившееся число на 2 и прибавить его к 10%.

Пример: 15% от 650

1. Находим 10% — 65.
2. Находим половину от 65 — это 32,5.
3. Прибавляем 32,5 к 65 и получаем 97,5.

Банальный трюк

Пожалуй, все мы натыкались на такой трюк:

Задумайте любое число. Умножьте его на 2. Прибавьте 12. Разделите сумму на 2. Вычтите из неё исходное число.

Вы получили 6, верно? Что бы вы ни загадали, вы всё равно получите 6. И вот почему:

1. 2x (удвоить число).
2. 2x + 12 (прибавить 12).
3. (2x + 12) : 2 = x + 6 (разделить на 2).
4. x + 6 − x (вычесть исходное число).

Этот трюк построен на элементарных правилах алгебры. Поэтому, если вы когда-нибудь услышите, что кто-то его загадывает, натяните свою самую надменную усмешку, сделайте презрительный взгляд и расскажите всем разгадку. ????

Магия числа 1 089

Этот трюк существует не одно столетие.

Запишите любое трёхзначное число, цифры которого идут в порядке уменьшения (к примеру, 765 или 974). Теперь запишите его в обратном порядке и вычтите его из исходного числа. К полученному ответу добавьте его же, только в обратном порядке.

Какое бы число вы ни выбрали, в результате получите 1 089.

Быстрые кубические корни

Для того чтобы быстро считать кубический корень из любого числа, понадобится запомнить кубы чисел от 1 до 10:

1	2	3	4	5	6	7	8	9	10
1	8	27	64	125	216	343	512	729	1 000

Как только вы запомните эти значения, находить кубический корень из любого числа будет элементарно просто.

Пример: кубический корень из 19 683

1. Берём величину тысяч (19) и смотрим, между какими числами она находится (8 и 27). Соответственно, первой цифрой в ответе будет 2, а ответ лежит в диапазоне 20+.
2. Каждая цифра от 0 до 9 появляется в таблице по одному разу в виде последней цифры куба.
3. Так как последняя цифра в задаче — 3 (19 683), это соответствует 343 = 7^3. Следовательно, последняя цифра ответа — 7.
4. Ответ — 27.

Примечание: трюк работает только тогда, когда исходное число является кубом целого числа.

Правило 70

• Чтобы найти число лет, необходимых для удвоения ваших денег, нужно разделить число 70 на годовую процентную ставку.
• Пример: число лет, необходимое для удвоения денег с годовой процентной ставкой 20%.
• 70 : 20 = 3,5 года

Правило 110

1. Чтобы найти число лет, необходимых для утроения денег, нужно разделить число 110 на годовую процентную ставку.
2. Пример: число лет, необходимое для утроения денег с годовой процентной ставкой 12%.
3. 110 : 12 = 9 лет

Математика — волшебная наука. Если даже такие простые трюки удивляют, то какие ещё фокусы можно придумать?

Источник: https://xakep.ru/2014/12/11/math-tricks/

Устный счет: техника быстрого счета в уме

Зачем считать в уме, если решить любую арифметическую задачу можно на калькуляторе. Современная медицина и психология доказывают, что устный счет — это тренаж для серых клеточек. Выполнять такую гимнастику необходимо для развития памяти и математических способностей.

Известно множество приёмов для упрощения вычислений в уме. Все, кто видел знаменитую картину Богданова-Бельского «Устный счёт», всегда удивляются — как крестьянские дети решают такую непростую задачу, как деление суммы из пяти чисел, которые предварительно ещё надо возвести в квадрат?

Оказывается, эти дети — ученики известного педагога-математика Сергея Александровича Рачицкого (он также изображен на картине). Это не вундеркинды — ученики начальных классов деревенской школы XIX века. Но все они уже знают приёмы упрощения арифметических расчетов и выучили таблицу умножения! Поэтому решить такую задачку этим детишкам вполне под силу!

Секреты устного счёта

Существуют приемы устного счета — простые алгоритмы, которые желательно довести до автоматизма. После овладения простыми приёмами можно переходить к освоению более сложных.

Прибавляем числа 7,8,9

Для упрощения вычислений числа 7,8,9 сначала надо округлять до 10, а затем вычитать прибавку. К примеру, чтобы прибавить 9 к двузначному числу, надо сначала прибавить 10, а затем вычесть 1 и т.д.

• Примеры:
• 56+7=56+10-3=63
• 47+8=47+10-2=55
• 73+9=73+10-1=82

Быстро складываем двузначные числа

Если последняя цифра двузначного числа больше пяти, округляем его в сторону увеличения. Выполняем сложение, из полученной суммы отнимаем «добавку».

1. Примеры:
2. 54+39=54+40-1=93
3. 26+38=26+40-2=64
4. Если последняя цифра двузначного числа меньше пяти, то складываем по разрядам: сначала прибавляем десятки, затем — единицы.
5. Пример:
6. 57+32=57+30+2=89
7. Если слагаемые поменять местами, то сначала можно округлить число 57 до 60, а потом вычесть из общей суммы 3:
8. 32+57=32+60-3=89

Складываем в уме трехзначные числа

Быстрый счет и сложение трехзначных чисел — это возможно? Да. Для этого надо разобрать трехзначные числа на сотни, десятки, единицы и поочередно их приплюсовать.

Пример:

249+533=(200+500)+(40+30)+(9+3)=782

Особенности вычитания: приведение к круглым числам

Вычитаемые округляем до 10, до 100. Если надо вычесть двузначное число, надо округлить его до 100, вычесть, а затем к остатку прибавить поправку. Это актуально если поправка невелика.

• Примеры:
• 67-9=67-10+1=58
• 576-88=576-100+12=488

Вычитаем в уме трехзначные числа

1. Если в свое время был хорошо усвоен состав чисел от 1 до 10, то вычитание можно производить по частям и в указанном порядке: сотни, десятки, единицы.
2. Пример:
3. 843-596=843-500-90-6=343-90-6=253-6=247 

Умножить и разделить

Моментально умножать и делить в уме? Это возможно, но без знания таблицы умножения не обойтись. Таблица умножения — это золотой ключик к быстрому счету в уме! Она применяется и при умножении, и при делении. Вспомним, что в начальных классах деревенской школы в дореволюционной Смоленской губернии (картина «Устный счет») дети знали продолжение таблицы умножения — с 11 до 19!

Хотя на мой взгляд достаточно знать таблицу от 1 до 10, чтобы мочь перемножать бо´льшие числа. Например:

15*16=15*10+(10*6+5*6)=150+60+30=240

Умножаем и делим на 4, 6, 8, 9

Овладев таблицей умножения на 2 и на 3 до автоматизма, сделать остальные расчеты будет проще простого.

Для умножения и деления двух- и трехзначных чисел применяем простые приёмы:

• умножить на 4 — это дважды умножить на 2;
• умножить на 6 — это значит умножить на 2, а потом на 3;
• умножить на 8 — это трижды умножить на 2;
• умножить на 9 — это дважды умножить на 3.

• Например:
• 37*4=(37*2)*2=74*2=148;
• 412*6=(412*2)·3=824·3=2472
• Аналогично:

• разделить на 4 — это дважды разделить на 2;
• разделить на 6 — это сначала разделить на 2, а потом на 3;
• разделить на 8 — это трижды разделить на 2;
• разделить на 9 — это дважды разделить на 3.

1. Например:
2. 412:4=(412:2):2=206:2=103
3. 312:6=(312:2):3=156:3=52

Как умножать и делить на 5

Число 5 — это половина от 10 (10:2). Поэтому сначала умножаем на 10, затем полученное делим пополам.

Пример:

326*5=(326*10):2=3260:2=1630

Еще проще правило деления на 5. Сначала умножаем на 2, а затем полученное делим на 10.

326:5=(326·2):10=652:10=65,2.

Умножение на 9

Чтобы умножить число на 9, необязательно его дважды умножать на 3. Достаточно его умножить на 10 и вычесть из полученного умножаемое число. Сравним, что быстрее:

• 37*9=(37*3)*3=111*3=333
• или
• 37*9=37*10 — 37=370-37=333

Также давно замечены частные закономерности, которые значительно упрощают умножение двузначных чисел на 11 или на 101. Так, при умножении на 11, двузначное число как бы раздвигается. Составляющие его цифры остаются по краям, а в центре оказывается их сумма.

Например: 24*11=264. При умножении на 101, достаточно приписать к двузначному числу такое же. 24*101= 2424. Простота и логичность таких примеров вызывает восхищение.

Встречаются такие задачи очень редко — это примеры занимательные, так называемые маленькие хитрости.

Счет на пальцах

Сегодня еще можно встретить много защитников «пальчиковой гимнастики» и методики устного счета на пальцах.

Нас убеждают, что учиться складывать и отнимать, загибая и разгибая пальцы — это очень наглядно и удобно. Диапазон таких вычислений очень ограничен.

Как только расчеты выходят за рамки одной операции возникают трудности: надо осваивать следующий прием. Да и загибать пальцы в эпоху айфонов как-то несолидно.

Например, в защиту «пальчиковой» методики приводится приём умножения на 9. Хитрость приёма такова:

• Чтобы умножить любое число в пределах первой десятки на 9, надо развернуть ладони к себе.
• Отсчитывая слева направо, загнуть палец, соответствующий умножаемому числу. К примеру, чтобы умножить 5 на 9, надо загнуть мизинец на левой руке.
• Оставшееся количество пальцев слева будет соответствовать десяткам, справа — единицам. В нашем примере — 4 пальца слева и 5 справа. Ответ: 45.

Да, действительно, решение быстрое и наглядное! Но это — из области фокусов. Правило действует только при умножении на 9.  А не проще ли, для умножения 5 на 9 выучить таблицу умножения?  Этот фокус забудется, а хорошо выученная таблица умножения останется навсегда.

Также существует еще множество подобных приемов с применением пальцев для каких-то единичных математических операций, но это актуально пока вы этим пользуетесь и тут же забывается при прекращении применения. Поэтому лучше выучить стандартные алгоритмы, которые останутся на всю жизнь. 

Устный счёт на автомате

• Во-первых, необходимо хорошо знать состав числа и таблицу умножения.
• Во-вторых, надо запомнить приемы упрощения расчётов. Как выяснилось, таких математических алгоритмов не так уж много.

• В-третьих, чтобы приём превратился в удобный навык, надо постоянно проводить краткие «мозговые штурмы» — упражняться в устных вычислениях, используя тот или иной алгоритм.

Тренировки должны быть короткими: решить в уме по 3-4 примера, используя один и тот же приём, затем переходить к следующему. Надо стремиться использовать любую свободную минутку — и полезно, и нескучно. Благодаря простым тренировкам все вычисления со временем будут совершаться молниеносно и без ошибок. Это очень пригодится в жизни и выручит в непростых ситуациях.

Источник: https://myintelligentkids.com/ustnyj-schet-texnika-bystrogo-scheta-v-ume